Zobraz hlavičku Znalecká kancelář, Akreditovaná zkušební laboratoř, projekty, posudky, dozory, výzkum, publikace, školení

Příklad závislosti velikosti tepelného toku na vzájemné poloze posuzovaných ploch

2005
Ing. Antonín Žák

Vezměme si dvě desky o šířce 30 m nacházející se ve vzdálenosti 10 m. Spodní deska bude představovat ledovou plochu a horní střechu. Rozdělme si tedy horní desku (střechu) na tři části o šířce pruhu 10 m (viz obrázek). Střední část střech tedy bude vodorovná. Segment střechy vlevo bude také vodorovný. Vpravo bude segment pootočen o 45° tak, aby představoval šikmou část obloukové střechy.
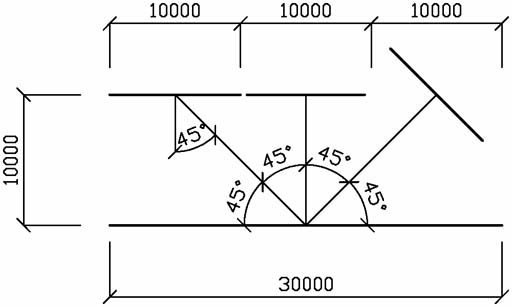
schéma střechy

Vezměme, že teploty a emisivity střešních segmentů budou stejné a teplota ledu bude po celé ploše konstantní. Pak středový segment bude vzdálený od ledové plochy 10 m, normály ledu i středového segmentu, ale i spojnice středů ploch budou vertikální, prostorový úhel bude roven nule, tudíž kosinus bude roven jedné. Tepelný tok bude tedy maximální a jeho velikost bude:

q = qn . 1 . 1 / 102 = qn . 0,01 W.m-2.K-1

U levého segmentu bude vzdálenost středu ledu a střechy 14,1 m, prostorový úhel bude 45° (cos 45° = 0,707). Výsledný tepelný tok tedy bude roven:

qn,1= qn . 0,707 . 0,707 / 14.12 = qn . 0,0025 W.m-2.K-1

U pravého segmentu bude vypadat příklad následovně. Vzdálenost středů ozařovaných ploch bude stejná 14,1 m, úhel mezi spojnicí středů a normálou ledové plochy bude 45° => cos 45° = 0,707, ale úhel mezi spojnicí středů a normálou segmentu střechy bude 0° => cos 0° = 1. Výsledný tepelný tok tedy bude:

qn,1= qn . 0,707 . 1 / 14.12 = qn . 0,0036 W.m-2.K-1

Je tedy patrné, že největší tepelný tok (vychlazování) je na střední segment. Dále z hodnot vyplývá, že u pravého segmentu dochází k většímu ochlazování než u segmentu levého, i když jsou ve stejné vzdálenosti.

Je ale pravdou, že by do výsledku měly vstoupit další vlivy (jako např. ohřívání od tribun), které eliminují mírné navýšení ochlazování oproti střechám plochým. To ve výsledku znamená, že se střešní konstrukce obloukové a ploché chovají při reálných poloměrech přibližně stejně - viz grafy 3 a 4 v článku Navrhování střech nevytápěných a neklimatizovaných zimních stadionů.